Conservation Laws and Pulse Propagation in Optical Metamaterials with Power-Law NLSE

By Samudrapom DamReviewed by Louis CastelAug 1 2025

A study recently published in Scientific Reports investigated soliton solutions to the generalized nonlinear Schrödinger equation (NLSE) with the parabolic law.

Significance of Soliton Theory

Nonlinear partial differential equations (PDEs) are a key area in modern mathematics, specifically since the 1950s with the emergence of soliton theory in the nonlinear phenomena research. Developed in 1960–1970 based on plasmas, water waves, and optical fibers, soliton theory plays a vital role in mathematical physics and applied mathematics, with applications in biology, communication, mathematics, chemistry, plasma physics, condensed matter physics, and fluid dynamics.

Nonlinear PDEs are common in many physical phenomena and are studied using various mathematical methods. A key research focus is pulse propagation modeling in waveguides to enhance transmitted signal quality. Many mathematical models represent the NLSE generalization, incorporating nonlinear dispersion, absorption, and propagation properties.

Metamaterials and Wave Phenomena

Complex materials with both real and negative dielectric permittivity and magnetic permeability have garnered significant research interest. Metamaterials with exceptional impact resistance, often made from combinations of metals and plastics, have become a major area of interest in optical metamaterials research. Their unique properties are driving significant discoveries in light science, with results that continue to surprise researchers.

Wave phenomena appear in many scientific and engineering fields through linear/nonlinear PDEs, including electromagnetism, optics, fluid mechanics, and quantum mechanics; and equations like Biswas-Milovic, Huxley, Fisher, and their combined forms; the Boiti-Leon-Pempinelli systems. Thus, the nonlinear PDE exploration has gained the attention of several researchers.

The Study

This paper used two analytical techniques to investigate several optical and other soliton solutions for the generalized NLSE with the parabolic nonlinear law. The analytical schemes are the improved 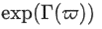function technique (IEFT) and the combined function technique (CSCFT). The study explored different exponential function solution sets for nonlinear models, employing two consistent integration standards to develop optical dark, combo, singular, periodic, and complex solutions. On applying Chupin Liu’s theorem to the black and grey optical solitons, researchers constructed new combined optical soliton solution sets of the model.

These solutions have growing applications in materials and building sciences, particularly in characterizing wave behavior in governing models. By selecting appropriate parametric values, the research visualized two-dimensional (2D), three-dimensional (3D), and density profiles to better understand the underlying physical phenomena. The investigation aimed to enhance current strategies for solving ordinary differential equations (ODEs) and PDEs. Additionally, a new conservation law theorem was introduced, marking a meaningful step forward in the theoretical study of nonlinear wave analysis.

Soliton propagation describes their movement in dispersion-managed fibers, where energy and trajectory of solitons are controlled. This propagation arises from a balance between self-phase modulation (SPM) and group-velocity dispersion (GVD). Group velocity is the velocity at which a wave’s power propagates in a medium. Although the velocity remains positive in passive media, it becomes negative around absorption lines over narrow bandwidths.

SPM represents a nonlinear phenomenon incorporating an instant light intensity shift for signal spectrum expansion. High optical intensity light beams shift phase in SPM amid perturbations in the medium’s refractive index. GVD is a dispersive medium characteristic in optics and is used to determine the impact of the medium on an optical pulse’s duration traveling through the medium. The GVD causes the pump’s spectral components to move at various velocities, resulting in a temporal pulse broadening.

Significance of the Work

The work explored traveling wave solutions of various types, including topological, singular, periodic, solitary, and single wave forms, related to the generalized Schrödinger equation. Two analytical techniques, the IEFT method and the CSCFT method, were applied to derive these solutions. In addition, the polynomial function method was employed to construct new analytical solutions, particularly rational solutions involving anti-kink solitary waves expressed using polynomials in �� and ��. The approaches used proved to be robust, efficient, and effective.

These analytical strategies facilitated the derivation of different soliton structures like periodic, single-shape solitons, kink-type, and dark soliton waves. The resulting solutions were visualized through 2D, 3D, and density plots to reveal their physical characteristics. Chupin Liu’s theorem was used to obtain new combined forms of grey and black optical solitons, adding to the variety of wave structures generated. Conservation laws were also derived using a newly proposed conservation theorem, supporting the mathematical integrity of the solutions.

The pictorial representations played a crucial role in understanding the behavior and dynamics of the obtained solutions, especially in contexts such as optical fiber signal analysis and nonlinear plasma material science.

In conclusion, the research provided valuable insights into nonlinear PDEs, with future goals including a more detailed stability analysis of solitons under the targeted model to deepen understanding of wave phenomena in complex media.

Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.