On-Chip Perovskite Polariton Parametric Oscillator with a Low Threshold

By Laura ThomsonDec 17 2021

Optical parametric oscillators (OPOs) have found extensive applications in spectroscopy, squeezed light generation, and correlated photons, as well as quantum information, such as for Ising machines and quantum random number generation. This article looks at Wu, J. et al.'s journal paper published in Advanced Photonics.

In the case of conventional systems, OPOs generally need non-centrosymmetric crystals (second-order nonlinearity) integrated into an external resonator that is resonant not only with the pump wavelength but also with the wavelength of produced signal and idler states.

It is possible to further tune generated signal and idler states by regulating the phase-matching condition by varying the angle or temperature of the nonlinear crystal or adjusting the pump wavelength. But such conventional OPOs often suffer from a high power threshold. This is because anisotropic crystals need rigorous birefringence phase matching requirements and often show limited high-order nonlinearity.

As a substitute, polaritonic systems built with hybridized exciton–photon quasi-particles as the basis show improved optical nonlinearity by binding photons with excitons, which ensures highly nonlinear operations with reduced power consumption. This paves a new path for nonlinear polaritonic devices.

This study discusses a low-threshold on-chip perovskite polariton parametric oscillator using all-inorganic CsPbBr₃ microcavities at ambient temperature. The signal at the ground state is obtained using the resonant excitation at different angles. This signal arises as a result of the polariton–polariton interactions that occur at ambient temperature. The results of this study offer a practical way toward embedded nonlinear polaritonic devices that exhibit low thresholds.

Methodology

The central perovskite integrated into a bottom distributed Bragg reflector (DBR) and a top DBR helps form the perovskite microcavity. As a first step, chemical vapor deposition (CVD) is used to grow the all-inorganic CsPbBr₃ single crystal film on a mica substrate.

Then, tape-transferring of the perovskite to the bottom DBR is performed, where the bottom DBR is made of 30.5 pairs of TiO₂/SiO₂. Subsequently, a PMMA spacer layer is deposited by spin-coating. Lastly, an electron beam evaporator is used to deposit 7.5 more pairs of TiO₂/SiO₂ as the top DBR.

The momentum-space photoluminescence (PL) mappings are quantified through a home-built angle-resolved spectroscopy configuration that includes the excitation, transparent stage, and detection in order together with Fourier optics at ambient temperature.

When it comes to the linear regime, the continuous-wave (CW) laser (457 nm) is used to pump the perovskite microcavity at normal incidence and a spot size of 10 μm². By contrast, in the case of the nonlinear regime, a pulsed laser (with a pulse width of 6 ns and a repetition rate of 20 Hz) with tunable wavelength serves as the excitation source.

In the experiment performed as part of this, as illustrated in Figure 1(a), the CsPbBr₃ single-crystal film developed by CVD shows a flat surface with powerful green fluorescence. Figure 1(b) shows a schematic description of the geometry of the polariton parametric oscillator, where the idler and signal can be produced along the k_x axis in far-field emission upon resonantly exciting the CsPbBr₃ microcavity with a critical (magic) angle along k_x.

Shown in Figure 1(c) is the microcavity’s angle-resolved photoluminescence spectrum in horizontal (H) polarization by excitation with a non-resonant CW laser (with a wavelength of 457 nm).

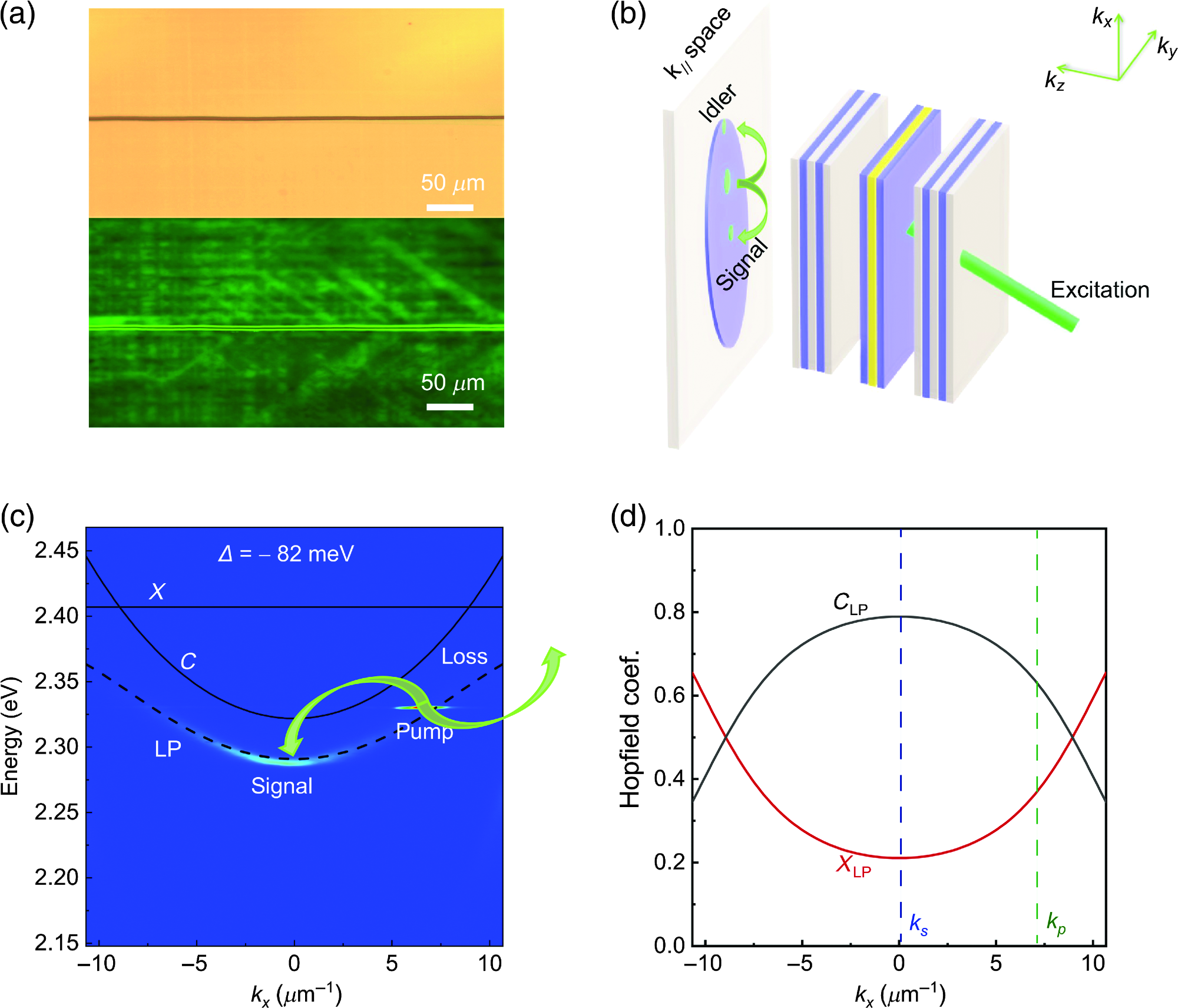
Figure 1. Schematic diagram and mechanism of polariton parametric oscillator in the perovskite microcavity. (a) Microscopy image and fluorescence microscopy image of the CsPbBr₃ perovskite single crystal. (b) Experimental geometry of the CsPbBr₃ perovskite microcavity, in which a thick CsPbBr₃ perovskite is sandwiched by two DBRs. (c) Angle-resolved photoluminescence spectrum of CsPbBr₃ microcavity along H polarization under CW excitations. The dashed black line displays the theoretical fitting dispersion of the LP dispersion; the solid black lines show the dispersions of uncoupled CsPbBr₃ perovskite exciton (X) and cavity photon mode (C); the detuning Δ is indicated in this figure. (d) Hopfield coefficients illustrating the exciton (X_LP) and photon (C_LP) fraction of the LP dispersion along x polarization; the blue vertical line denotes the signal state polariton (k_s); the green vertical line represents the pump state polariton (k_p). Image Credit: Wu, et al. 2021

A pulsed nanosecond laser with a wavelength of 533 nm is used for further resonant excitation of the system to achieve the nonlinear regime in the transmission configuration. In this case, the resonant excitation is matched with the high-k state in the polariton dispersion by spectrally tuning with a negative detuning of Δ = −82 meV.

Figure 2(a) shows the polariton energy dispersion along k_x without a clear signal state at the pump power of 0.5 P_th based on the dispersions illustrated in Figure 1(c). Figure 2(b) illustrates the k_x–k_y far-field emission depicting the strong pump state along k_x. Increasing pump power leads to a more efficient polariton scattering, which stimulates polariton parametric oscillation. This oscillation causes strong emission when the ground state is the signal state.

Figure 2(c) illustrates that at the pump power of 3 P_th, the signal state is at the ground state of the dispersion. By contrast, the idler state at k_x = 13.6 μm⁻¹ could not be observed (partially because the idler’s wavevector was beyond the collected range). When it comes to the polariton–polariton nonlinear pump term, the theoretical calculations illustrated in Figure 2(e)–2(h) are in good agreement with the experimental values shown in Figures 2(a)–2(d), respectively.

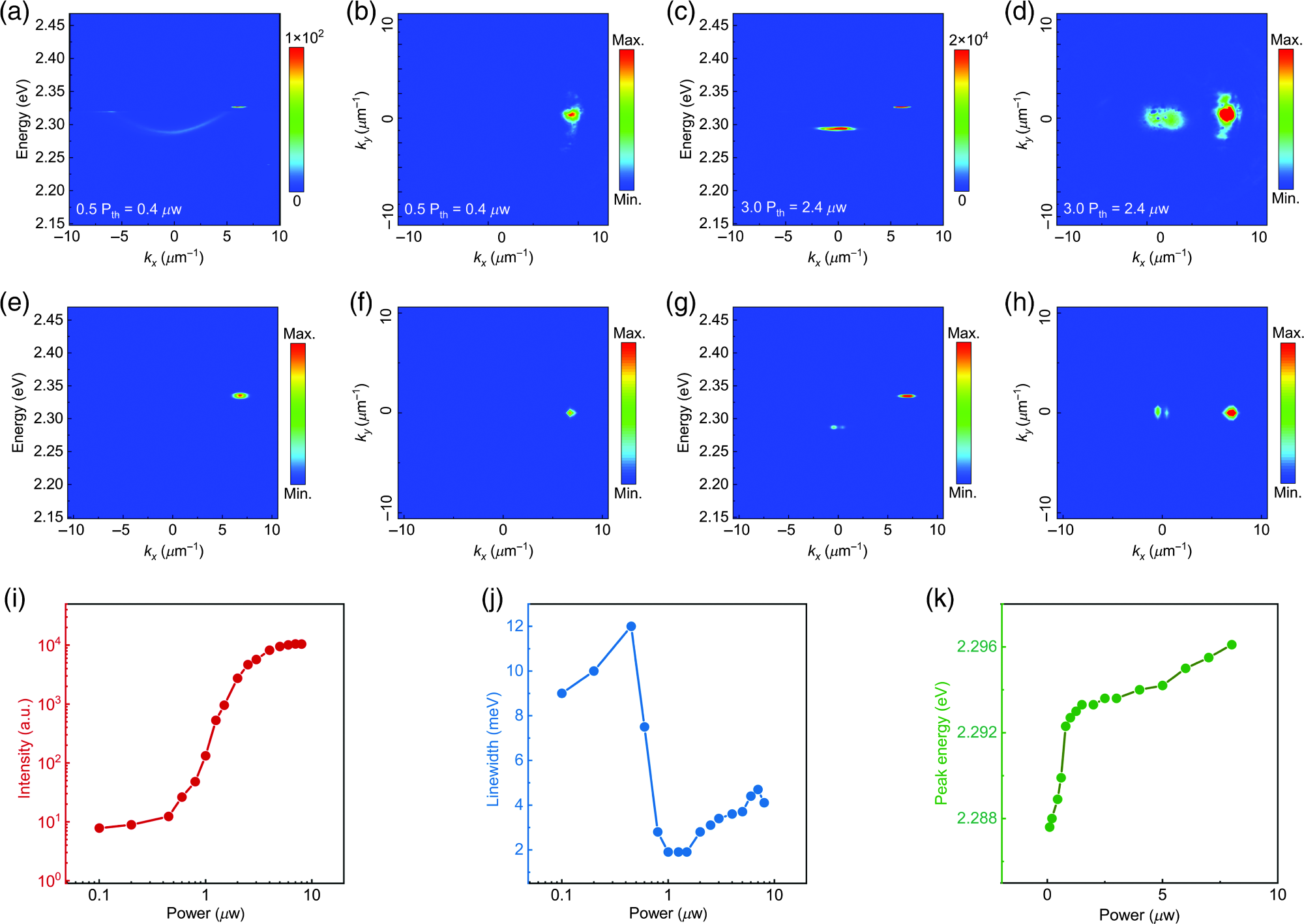
Figure 2. Observation and characterizations of polariton oscillation at room temperature. Experimental far-field emission of (a) energy–k_x and (b) k_x–k_y at the pump power of 0.5 P_th. Experimental far-field emission of (c) energy–k_x and (d) k_x–k_y at the pump power of 3 P_th. Theoretically calculated far-field emission of (e) energy–k_x and (f) k_x–k_y at the pump power of 0.5 P_th. Theoretically calculated far-field emission of (g) energy–k_x and (h) k_x–k_y at the pump power of 3 P_th. (i) Signal-state k_s emission intensity as a function of pump k_p fluence in a log–log scale, demonstrating a super-linear increase by three orders of magnitude near threshold. (j) Signal-state k_s emission linewidth as a function of pump k_p fluence along with a sharp narrowing linewidth from 12 to 2 meV at the threshold. (k) Signal-state k_s emission peak energy with a continuous blueshift trend. Image Credit: Wu, et al. 2021

Figures 3(a)–3(c) show the resonantly excited pump states, where a slight blueshift can be observed between polariton dispersion at higher k and the pump states. This blueshift emerges from the higher exciton fraction. Figures 3(a)–3(c) illustrate the parametric oscillation thresholds plotted as a function of pump states in Figures 3(d)–3(f), respectively.

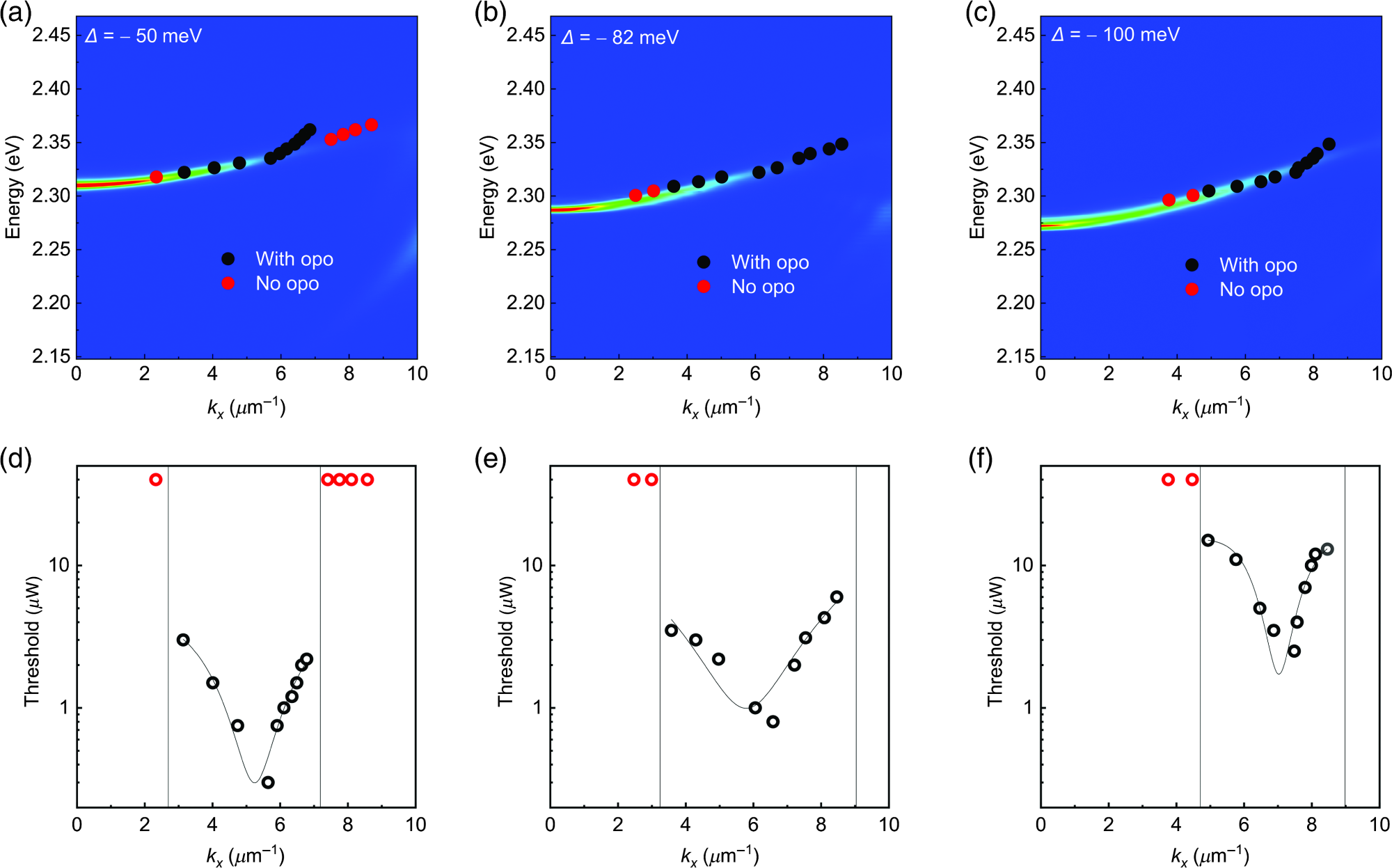
Figure 3. Characterizations of polariton oscillator versus pump states for three samples with different detunings Δ = −50, −82, −100 meV, respectively. (a)–(c) The pump state is tuned with energy and angle to resonantly excite the LP dispersion for detunings (a) Δ = −50 meV, (b) Δ = −82 meV, and (c) Δ = −100 meV. (d)–(f) The energy conversion threshold as a function of pump state angle for detunings (d) Δ = −50 meV, (e) Δ = −82 meV, and (f) Δ = −100 meV. The lowest energy conversion threshold peaks at (d) P_th = 0.3 μW, (e) P_th = 0.8 μW, and (f) P_th = 2.5 μW, respectively. The black circles denote the occurrence of OPO, whereas the red circles represent cases where the OPO was not present. Image Credit: Wu, et al. 2021

The polarization dependence of the signal in the new perovskite microcavity was analyzed further. The intrinsic anisotropy of the perovskite crystal makes the LP dispersion exhibit a linearly polarized splitting, upon being excited by a CW laser (457 nm), at k = 0, E_sV = 2.296 eV along V polarization, and E_sH = 2.287 eV along H polarization illustrated in Figure 4(a).

Figure 4(b) illustrates the high H linearly polarized pump following the DBR microcavity. When this H polarized pump is at a critical point—i.e., E_p = 2.326 eV (a wavelength of 533 nm) and k_x = 6.8 μm⁻¹—Malus’s law helps detect and fit the polar plot of the signal, exhibiting high H linear polarization as shown in Figure 4(c).

Moreover, as shown in Figure 4(d), the system is excited by a left circular pump close to the critical angle—E_p = 2.326 eV (a wavelength of 533 nm) and k_x = 6.8 μm⁻¹, where the width of the pump in k space is sufficient to cover the V polarized polariton mode and the H polarized polariton mode at the same time.

For the H polariton mode, the pump angle is the critical (magic) angle, whereas it is slightly larger in the case of the V polariton mode, which makes the intensity of the H polarized signal nearly two times stronger compared to the V polarized signal shown in Figure 4(e).

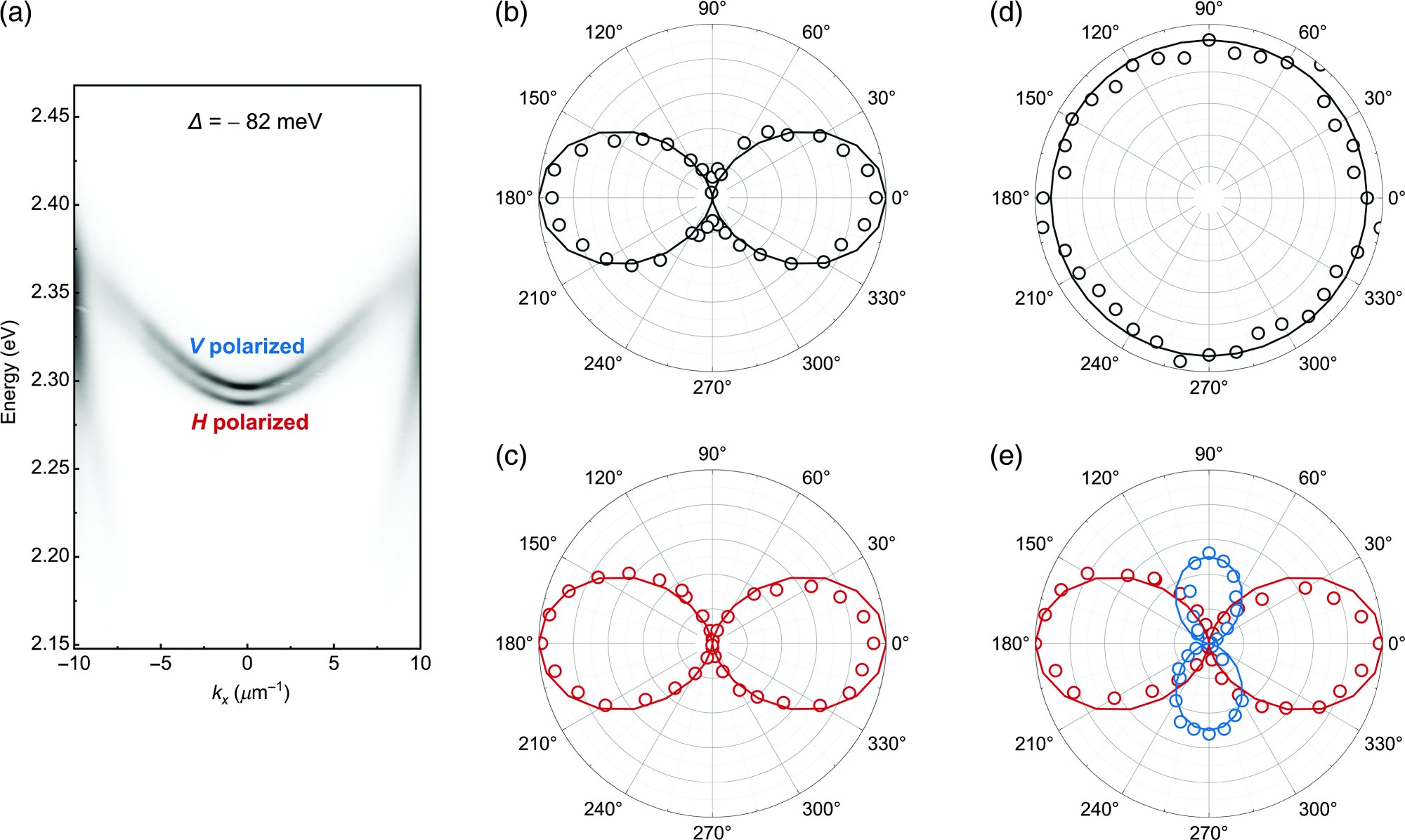
Figure 4. Polarization dependence of the polariton parametric oscillator. (a) Angle-resolved photoluminescence spectrum of CsPbBr₃ microcavity along V polarization and H polarization under CW excitation. (b) Polar plot of the H polarized pump excited at E_p = 2.326 eV (533 nm), centered k_x = 6.8 μm⁻¹ (black circle dots), and fitting function (black solid line) fαcos² θ. (c) Under excitation of (b), polar plot of the measured polarization emission of the signal state at E_sH = 2.287 eV, k_x = 0 μm⁻¹ (red circle dots) and fitting function (red solid line) fαcos² θ. (d) Polar plot of the left circularly polarized pump excited at E_p = 2.326 eV (533 nm), centered k_x = 6.8 μm⁻¹ (black circle dots), as well as a fitting constant function (continuous line). (e) Under excitation of (d), polar plot of the measured polarization emission of the signal state at E_sH = 2.287 eV, k_x = 0 μm⁻¹ (red circle dots), and fitting function (red solid line) fαcos² θ; at E_sV = 2.296 eV, k_x = 0 μm⁻¹ (blue circle dots), and fitting function (blue solid line) fαcos² (θ + 90 deg). Image Credit: Wu, et al. 2021

Conclusion

In this study, resonant excitation was implemented at a critical (magic) angle to theoretically and experimentally find the non-degenerate polariton parametric oscillator at ambient temperature in perovskite exciton-polaritons.

The findings correlate with the spontaneous parametric down-conversion over different angles. At the same time, the strong anisotropy of perovskite leads to a split in the signal state into two non-degenerate orthogonal linear polarizations. This study unravels an alternative route for achieving nonlinear polaritonic devices with a lower threshold.

Journal Reference:

Wu, J., Su, R., Fieramosca, A., Ghosh, S., Zhao, J., Liew, T. C. H., Xiong, Q. (2021) Perovskite polariton parametric oscillator. Advanced Photonics, 3(5), p. 055003. Available online: https://www.spiedigitallibrary.org/journals/advanced-photonics/volume-3/issue-05/055003/Perovskite-polariton-parametric-oscillator/10.1117/1.AP.3.5.055003.full?SSO=1.

References and Further Reading

1. Giordmaine, J A & Miller, R C (1965) Tunable Coherent Parametric Oscillation in LiNbO₃ at Optical Frequencies. Physical Review Letters, 14(24), pp. 973–976. doi.org/10.1103/PhysRevLett.14.973.
2. Wu, L.-A., et al. (1986) Generation of squeezed states by parametric down conversion. Physical Review Letters, 57(20), pp. 2520–2523. doi.org/10.1103/PhysRevLett.57.2520.
3. Jabri, H & Eleuch, H (2020) Interaction of a dipolariton system with squeezed light from a parametric down-conversion process. Physical Review A, 101(5), p. 053819. doi.org/10.1103/PhysRevA.101.053819.
4. Förtsch, M., et al. (2013) A versatile source of single photons for quantum information processing. Nature Communications, 4(1), p. 1818. doi.org/10.1038/ncomms2838.
5. Guo, X., et al. (2017) Parametric down-conversion photon-pair source on a nanophotonic chip. Light: Science & Applications, 6(5), p. e16249. doi.org/10.1038/lsa.2016.249.
6. Lu, X., et al. (2019) Chip-integrated visible–telecom entangled photon pair source for quantum communication. Nature Physics, 15, pp. 73–381. doi.org/10.1038/s41567-018-0394-3.
7. Inagaki, T., et al. (2016) Large-scale Ising spin network based on degenerate optical parametric oscillators. Nature Photonics, 10(6), pp. 415–419. doi.org/10.1038/nphoton.2016.68.
8. Bruch, A. W., et al. (2019) On-chip χ⁽²⁾ microring optical parametric oscillator. Optica, 6(10), pp. 1361–1366. doi.org/10.1364/OPTICA.6.001361.
9. Breunig, I., et al. (2016) Three-wave mixing in whispering gallery resonators. Laser Photonics & Reviews, 10(4), pp. 569–587. doi.org/10.1002/lpor.201600038.
10. Lin, Z.-G., et al. (2008) Characterization and properties of novel infrared nonlinear optical crystal CsGe (Br_x Cl_1−x)₃. Inorganic Chemistry, 47(7), pp. 2362–2367. doi.org/10.1021/ic7011777.
11. Xu, J., et al. (2020) Halide perovskites for nonlinear optics. Advanced Materials, 32(3), p. 1806736. doi.org/10.1002/adma.201806736.
12. Zhou, Y., et al. (2020) Nonlinear optical properties of halide perovskites and their applications. Applied Physics Reviews, 7(4), p. 041313. doi.org/10.1063/5.0025400.
13. Kippenberg, T. J., et al. (2004) Kerr-nonlinearity optical parametric oscillation in an ultrahigh-Q toroid microcavity. Physical Review Letters, 93(8), p. 083904. doi.org/10.1103/PhysRevLett.93.083904.
14. Fürst, J. U., et al. (2010) Low-threshold optical parametric oscillations in a whispering gallery mode resonator. Physical Review Letters, 105(26), p. 263904. doi.org/10.1103/PhysRevLett.105.263904.
15. Beckmann, T., et al. (2011) Highly tunable low-threshold optical parametric oscillation in radially poled whispering gallery resonators. Physical Review Letters, 106(14), p. 143903. doi.org/10.1103/PhysRevLett.106.143903.
16. Sayson, N. L. B., et al. (2019) Octave-spanning tunable parametric oscillation in crystalline Kerr microresonators. Nature Photonics. 13 (10), pp.701–706. doi.org/10.1038/s41566-019-0485-4.
17. Lu, X., et al. (2019) Milliwatt-threshold visible–telecom optical parametric oscillation using silicon nanophotonics. Optica, 6 (12), pp. 1535–1541. doi.org/10.1364/OPTICA.6.001535.
18. Lu, J., et al. (2021) Ultralow-threshold thin-film lithium niobate optical parametric oscillator. Optica, 8(4), pp. 539–544. doi.org/10.1364/OPTICA.418984.
19. Trovatello, C., et al. (2021) Optical parametric amplification by monolayer transition metal dichalcogenides. Nature Photonics, 15(1), pp. 6–10. doi.org/10.1038/s41566-020-00728-0.
20. Deng, H., et al. (2010) Exciton–polariton Bose–Einstein condensation. Reviews of Modern Physics, 82(2), pp. 1489–1537. doi.org/10.1103/RevModPhys.82.1489.
21. Sanvitto, D & Kéna-Cohen, S (2016) The road towards polaritonic devices. Nature Materials, 15(10), pp. 1061–1073. doi.org/10.1038/nmat4668.
22. Sanvitto D & Kéna-Cohen, S (2016) The road towards polaritonic devices. Nature Materials, 15(10), pp.1061–1073. doi.org/10.1038/nmat4668.
23. Baumberg, J. J., et al. (2000) Parametric oscillation in a vertical microcavity: a polariton condensate or micro-optical parametric oscillation. Physical Review B, 62(24), pp. R16247–R16250. doi.org/10.1103/PhysRevB.62.R16247.
24. Savvidis, P. G., et al. (2000) Angle-resonant stimulated polariton amplifier. Physical Review Letters, 84(7), pp. 1547–1550. doi.org/10.1103/PhysRevLett.84.1547.
25. Saba, M., et al. (2001) High-temperature ultrafast polariton parametric amplification in semiconductor microcavities. Nature, 414(6865), pp. 731–735. doi.org/10.1038/414731a.
26. Dasbach, G., et al. (2005) Polarization inversion via parametric scattering in quasi-one-dimensional microcavities. Physical Review B, 71(16), p.161308. doi.org/10.1103/PhysRevB.71.161308.
27. Diederichs, C., et al. (2006) Parametric oscillation in vertical triple microcavities. Nature, 440(7086), pp. 904–907. doi.org/10.1038/nature04602.
28. Kuznetsov, A. S., et al. (2020) Dynamically tuned arrays of polariton parametric oscillators. Optica, 7(12), pp. 1673–1681. doi.org/10.1364/OPTICA.399747.
29. Ardizzone, V., et al. (2012) Bunching visibility of optical parametric emission in a semiconductor microcavity. Physical Reviews B, 86(4), p. 041301. doi.org/10.1103/PhysRevB.86.041301.
30. Lecomte, T., et al. (2013) Optical parametric oscillation in one-dimensional microcavities. Physical Reviews B, 87(15), p. 155302. doi.org/10.1103/PhysRevB.87.155302.
31. Xie, W., et al. (2012) Room-temperature polariton parametric scattering driven by a one-dimensional polariton condensate. Physical Reviews Letters, 108(16), p. 166401. doi.org/10.1103/PhysRevLett.108.166401.
32. Wu, J., et al. (2021) Nonlinear parametric scattering of exciton polaritons in perovskite microcavities. Nano Letters, 21(7), pp. 3120–3126. doi.org/10.1021/acs.nanolett.1c00283.
33. Quan, L. N., et al. (2018) Perovskites for light emission. Advance Materials, 30(45), p. 1801996. doi.org/10.1002/adma.201801996.
34. Xing, J., et al. (2016) High-efficiency light-emitting diodes of organometal halide perovskite amorphous nanoparticles. ACS Nano, 10(7), pp. 6623–6630. doi.org/10.1021/acsnano.6b01540.
35. Veldhuis, S. A., et al. (2016) Perovskite materials for light-emitting diodes and lasers. Advanced Materials, 28(32), pp. 6804–6834. doi.org/10.1002/adma.201600669.
36. Zhang, Q., et al. (2021) Halide perovskite semiconductor lasers: materials, cavity design, and low threshold. Nano Letters, 21(5), pp. 1903–1914. doi.org/10.1021/acs.nanolett.0c03593.
37. Ahmadi, M., et al. (2017) A review on organic–inorganic halide perovskite photodetectors: device engineering and fundamental physics. Advanced Materials, 29(41), p. 1605242. doi.org/10.1002/adma.201605242.
38. Krishnakanth, K. N., et al. (2018) Broadband femtosecond nonlinear optical properties of CsPbBr₃ perovskite nanocrystals. Optics Letters, 43(3), pp. 603–606. doi.org/10.1364/OL.43.000603.
39. Zhou, F., et al. (2019) 2D perovskites with giant excitonic optical nonlinearities for high-performance sub-bandgap photodetection. Advanced Materials, 31(48), 1904155. doi.org/10.1002/adma.201904155.
40. Wu, L., et al. (2018) Perovskite CsPbX₃ a promising nonlinear optical material and its applications for ambient all-optical switching with enhanced stability. Advanced Optical Materials, 6(19), p.1800400.
41. Su, R., et al. (2017) Room-temperature polariton lasing in all-Inorganic perovskite nanoplatelets. Nano Letters, 17(6), pp. 3982–3988. doi.org/10.1021/acs.nanolett.7b01956.
42. Su, R., et al. (2018) Room temperature long-range coherent exciton polariton condensate flow in lead halide perovskites. Science Advances, 4(10), p. eaau0244. doi.org/10.1126/sciadv.aau0244.
43. Su, R., et al. (2021) Perovskite semiconductors for room-temperature exciton-polaritonics. Nature Materials, 20(10), pp. 1315–1324. doi.org/10.1038/s41563-021-01035-x.
44. Su, R., et al. (2021) Optical switching of topological phase in a perovskite polariton lattice. Science Advances, 7(21), p. eabf8049. doi.org/10.1126/sciadv.abf8049.
45. Fieramosca, A., et al. (2019) Two-dimensional hybrid perovskites sustaining strong polariton interactions at room temperature. Science Advances, 5(5), p. eaav9967. doi.org/10.1126/sciadv.aav9967.
46. Romanelli, M., et al. (2007) Four wave mixing oscillation in a semiconductor microcavity: generation of two correlated polariton populations. Physical Review Letters, 98(10), p. 106401. doi.org/10.1103/PhysRevLett.98.106401.
47. Ha, S. T., et al. (2014) Synthesis of organic–inorganic lead halide perovskite nanoplatelets: towards high-performance perovskite solar cells and optoelectronic devices. Advanced Optical Materials, 2(9), pp. 838–844. 
48. Zhang, Q., et al. (2016) High-quality whispering-gallery-mode lasing from cesium lead halide perovskite nanoplatelets. Advanced Functional Materials, 26(34), pp. 6238–6245. doi.org/10.1002/adfm.201601690.
49. Whittaker, D. M., et al. (2005) Effects of polariton-energy renormalization in the microcavity optical parametric oscillator. Physical Review B, 71(11), p. 115301. doi.org/10.1103/PhysRevB.71.115301.
50. Lagoudakis, P. G., et al. (2002) Stimulated spin dynamics of polaritons in semiconductor microcavities. Physical Review B, 65(16), p. 161310. doi.org/10.1103/PhysRevB.65.161310.
51. Su, R., et al. (2020) Observation of exciton polariton condensation in a perovskite lattice at room temperature. Nature Physics, 16(3), pp. 301–306. doi.org/10.1038/s41567-019-0764-5.