The development of cryptographic keys for traditional and quantum cryptography systems depends on random numbers. Numerous studies have been conducted on high-bandwidth chaotic semiconductor lasers for high-rate random number generation.
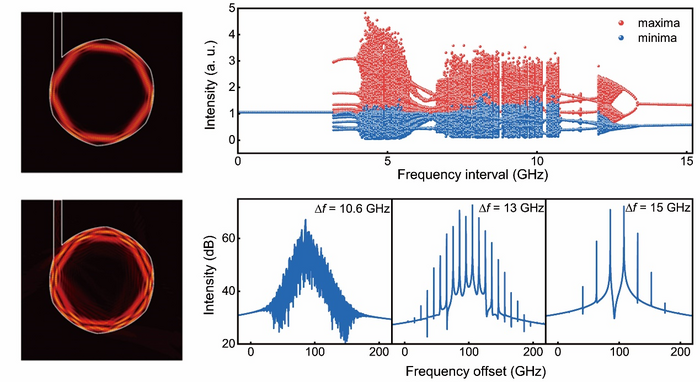Bifurcation of the extrema for the temporal output waveform versus dual-mode frequency interval (upper right) and ptical spectra of chaos, period-two, and period-one states at mode frequency interval Δf =10.6, 13, and 15 GHz, respectively (lower right). Image Credit: Chun-Guang Ma, Jin-Long Xiao, Zhi-Xiong Xiao, Yue-De Yang, and Yong-Zhen Huang
Traditional methods for chaotic lasers with external feedback have limitations, including a time-delay signature, sensitivity to perturbation parameters, and complicated modification for chaotic output realization.
Because of its reliable and straightforward design, a chaotic solitary laser without external disturbances is a popular arrangement for generating random numbers.
A group of researchers led by Professor Yong-Zhen Huang from the State Key Laboratory of Integrated Optoelectronics, Institute of Semiconductors, Chinese Academy of Sciences, Beijing, China, and the Center of Material Science and Optoelectronic Engineering, University of Chinese Academy of Sciences, Beijing, China, have proposed a brand-new approach to control the temporal output of a single semiconductor microlaser by nonlinear means in a new paper published in Light Science & Application.
Without external optical or electrical perturbations, the deformed microcavity laser’s total output produces chaotic output, enabling the creation of a simple, manageable, and reliable random signal generator.
It was intended for the Circular-Sided Hexagonal Microresonator (CSHM) to improve passive mode Q factors to implement dual-mode lasing with the adjustable frequency interval. Using a single CSHM laser, nonlinear dynamical states such as chaotic and period-oscillation states were achieved.
Directly from the entire output intensity of the microlaser, which was limited to 10 Gb/s by the tools utilized, physical random numbers were derived and verified by statistical tests. A practical and reliable method for generating random numbers quickly is provided by a single microcavity laser with chaotic total output intensity.
To consider the internal mode interaction, including mode coupling, a rate equation model built on field equations is set up. Due to mode beating, which improves the mode interaction, dual-mode lasing of the fundamental and first-order transverse modes ensures significant carrier oscillation inside the laser cavity.
The rate equation can be used to predict chaotic dual-mode lasing lasers without the use of outside disturbance.
The study team stated, “In a dual-mode lasing microlaser, mode beating can lead to oscillations of the photon density and carrier density caused by stimulated emission, especially as the mode interval is close to the laser relaxation oscillation frequency. The oscillation of the carrier density will result in side peaks for lasing modes as under external electric modulation, and lead to nonlinear coupling for the two lasing modes because the oscillation frequency is the frequency interval of the two lasing modes.”
They added, “The procedure in revealing the underlying mechanism of the internal interaction between two transverse modes gives a new understanding of the nonlinear dynamical process in the semiconductor microlasers.”
“Although the random bits generated at a bit rate of 10 Gbit s–1 (5 GS s–1 × 2 bits) is not much high, which is mainly limited by the instruments used in the test, we expect to realize higher bandwidth of random bits,” further stated the team.
The team concluded, “There is still much room to improve the random number rate of spontaneous chaotic microcavity lasers. we have effectively improved the chaotic bandwidth of chaotic lasers through the optimal design of resonant cavity, which is expected to generate higher rate physical random numbers under higher bandwidth chaotic signals. In the future, with the development of optoelectronic integration technology, spontaneous chaotic lasers are expected to achieve convenient and portable miniaturized random number generators.”
Journal Reference:
Ma, C. G, et al. (2022) Chaotic microlasers caused by internal mode interaction for random number generation. Light: Science & Applications. doi:10.1038/s41377-022-00890-w.