May 12 2021
In relativistic spacetime, one of the most fundamental structural aspects is the description of how distances and time are modified by motion.
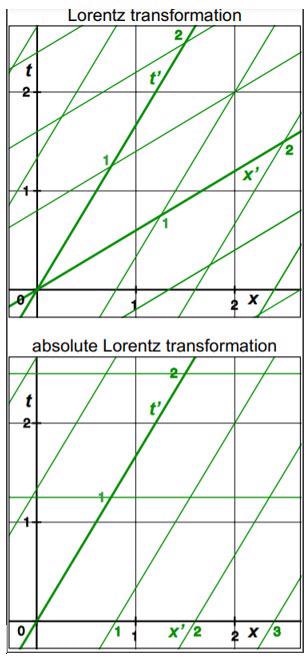
Image Credit: World Scientific.
The concept of unique relativity explains a spacetime framework for linear constant motion where time dilates and extends contract in response to movement. This spacetime framework is explained by the Lorentz transformation, which covers mathematical formulas that explain how distance and time are modified between moving reference frames.
This Lorentz transformation further explains how a stationary observer sees time in the moving reference frame to be offset with distance. Differential simultaneity is generated by the offsetting of time with the distance between the reference frames. In differential simultaneity, events that are concurrent for one observer will not be concurrent for a second observer moving in relation to the first observer.
With regard to rotating frames, the nature of spacetime has not been determined at the most basic level of defining the transformation that precisely explains the simultaneity framework and the relativistic effects.
The literature contains four distinct rotational relativistic transformations—the Langevin metric, Franklin transformation, Post transformation, and the absolute Lorentz transformation (ALT) in its rotational form.
Establishing which transformation precisely describes the experimental data would denote the spacetime framework existing in real-world rotating frames. Interpreting this crucial data has broad applicability because most of the visible matter in the Universe is in rotational motion, inclusive of the rotating Earth.
Langevin metric is the most extensively cited rotational transformation. This metric was initially explained in 1921. But over the years, the Langevin metric has been used for explaining relativity in rotating frames in an infinite number of research papers and textbooks. But to date, the Langevin metric has never been evaluated with experimental data that has enough resolution to differentiate it from the other crucial rotational transformations.
The transformation’s combination of simultaneity framework and relativistic effects influences the propagation of light. The four transformations have varying predictions for the rotating-frame two-way speed of light, one-way speeds of light, and the Sagnac effect.
The new study directly derives the optical predictions for every transformation from their transformation equations, with many of the predictions not formerly reported in the literature. The predictions are subsequently compared to the latest high-resolution optical experimental data.
Optical resonator data available on the two-way speed of light is one of the maximum resolution scientific measurements, with as high as 10-18 resolutions. This high resolution is needed to differentiate between the transformation predictions.
The new study showed that ALT and the Franklin transformation prediction of the continuous two-way speed of light, c, corresponds with the optical resonator data, whereas the Langevin metric and Post transformation predictions are canceled by the data.
The failure of Post transformation and the Langevin metric to correspond with optical resonator data is demonstrated to be caused by their exhibiting no (or no net) length contraction in the rotating frame. On the other hand, the ALT and Franklin transformations show length contraction, which enables their precise predictions for the two-way speed of light.
The Sagnac effect has lower resolutions of 10-8 and data on this effect is compatible with the Sagnac effect predictions of the Post transformation, ALT transformations, and Langevin metric, but not compatible with the Franklin transformation, which estimates no Sagnac effect.
The failure of the Franklin transformation to create an overt Sagnac effect is demonstrated to be caused by its integration of differential simultaneity. By contrast, the other three transformations integrate absolute simultaneity where time is not offset with distance, which enables overt Sagnac effects. ALT is, therefore, the only transformation that precisely explains the complete range of relativistic optical data.
Various publications have suggested mechanisms to integrate differential simultaneity into rotating frames to enable the creation of an overt Sagnac effect. But such mechanisms tend to create alternate Sagnac effect equations.
The latest study demonstrates that such alternate Sagnac effect equations indicate two-way speeds of light that are canceled by the high-resolution optical resonator data. On the other hand, ALT estimates the traditional Sagnac effect, implying the constant two-way speed of light, c.
The research work also shows that the ALT rotational transformation precisely estimates both non-optical rotating-frame relativistic observations and high-resolution optical data. This study indicates that the ALT rotational transformation explains the fundamental framework of spacetime in rotating frames.
This explains that rotating-frame spacetime is defined by the relativistic effects of length contraction and time dilation within an absolute simultaneity framework where time is not offset with distance.
Journal Reference:
Kipreos E T & Balachandranm, R S (2021) Assessment of the relativistic rotational transformations. Modern Physics Letters A.