Sep 20 2016
Devices based on light, rather than electrons, could revolutionize the speed and security of our future computers. However, one of the major challenges in today's physics is the design of photonic devices, able to transport and switch light through circuits in a stable way. Sergej Flach, Director of the Center for Theoretical Physics of Complex Systems, within the Institute for Basic Science (IBS) and colleagues from the National Technical University of Athens and the University of Patras (Greece) have studied how to achieve a more stable propagation of light for future optical technologies. Their model was recently published in Scientific Reports.
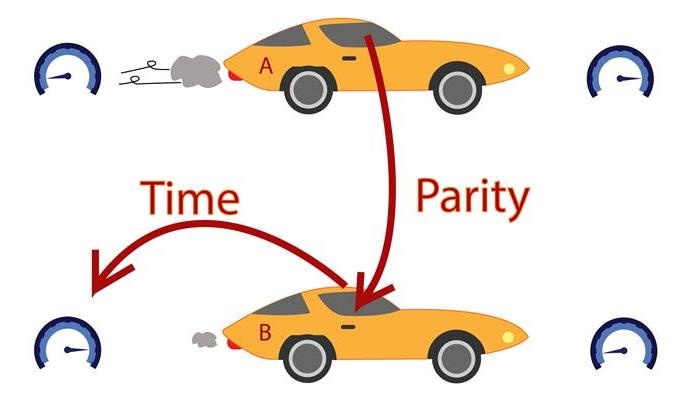Simplification to represent PT (Parity-Time) symmetry. Imagine a situation where two cars are traveling at the same speed at some instant in time, but car A is speeding up, and car B is slowing down. In order to go at the same speed, you can jump from one car to the other (Parity reversal) and back in time (Time reversal). (Graphics modified from freepiks).
Optical fibers can carry a large amount of information and are already used in many countries for communications via phone, internet and TV. However, when light travels long distances through these fibers, it suffers from losses and leakages, which could lead to a loss of information. In order to compensate for this problem, amplifiers are positioned at specific intervals to amplify the signal. For example, amplifiers are needed in submarine communications cables that allow the transfer of digital data between all continents (except for Antarctica). Researchers have tried to build fibers where the signal is stable along the pathway and does not need amplifiers, using the so-called “PT symmetry”. P stands for parity reversal and T for time reversal.
The PT symmetry can be simplified with an example. Imagine a situation where two cars are traveling at the same speed at some instant in time. However, one car is speeding up and the other one is slowing down. Using parity reversal (P) we exchange one car for the other. Using time reversal (T) we go back in time. If you are in the car that is accelerating, you can jump to the car that is slowing down (P) and you also go back in time (T). As a result, you will end up with the same speed as the accelerating car. The cars are like light waves inside the optical fibers and the speed is a representation of the intensity of light. The jumping symbolizes of the transfer of light from one fiber to another, which happens when the light waves propagating in each fiber overlap partially with each other, through a phenomenon called tunneling.
The PT symmetry idea is that one can carefully balance the intensity of light inside the fibers and achieve a stable propagation. Researchers expected PT symmetry to be the solution to achieve stable propagation in all-optical devices (diodes, transistors, switches etc.). However, stable propagation is still a challenge because the PT symmetry conditions have to be balanced extremely carefully, and because the material of the fibers reacts and destroys the exact balance. In the example of the cars, in order to achieve perfect PT symmetry, you would need really identical cars and street conditions. Reality is of course much different.
The team led by IBS found that the stability of light propagation can be achieved by breaking the PT symmetry in a controlled way. In the example of the cars, you would have to choose two cars that are actually different (for example, one has a better engine than the other), but you choose the differences deliberately.
“You have the potential to realize a lot of the items of the wish-list of the PT symmetry, by breaking the PT symmetry. But you have to break it in the right way,” explains Professor Flach. “Now we know how to tune the characteristics of the fiber couplers to achieve a long-lasting constant light propagation.”
Attached files
Simplification to represent PT (Parity-Time) symmetry. Imagine a situation where two cars are traveling at the same speed at some instant in time, but car A is speeding up, and car B is slowing down. In order to go at the same speed, you can jump from one car to the other (Parity reversal) and back in time (Time reversal). The cars are like the light waves inside the fiber, the speed of the cars is a representation of the intensity of light and the jump symbolizes a phenomenon called tunneling. (Graphics modified from freepiks).
No matter from which fiber the light is launched (core 1 in the graph on the left, or core 2 in the left of the right), the result is a stable wavelight.