A propagating light beam is commonly known as propagating electromagnetic radiation within the field of physical optics. The direction of propagation is horizontal to the direction of the electric and magnetic field vectors, while the polarizing direction of light is understood to be the direction of the electrical vector component.
As long as the route of the electrical field remains consistent throughout this propagation, light will be polarized directly.
This illustrates that this electric field vector’s perpendicular components are in phase, or there is no instance of phase variation between them (Figure A).
Should a 90° phase difference occur between these perpendicular components, the light will be circularly polarized (Figure B). Where the two components exhibit minimal phase variation, light is often polarized elliptically (Figure C).
Figures A, B, and C provide examples of light polarization.
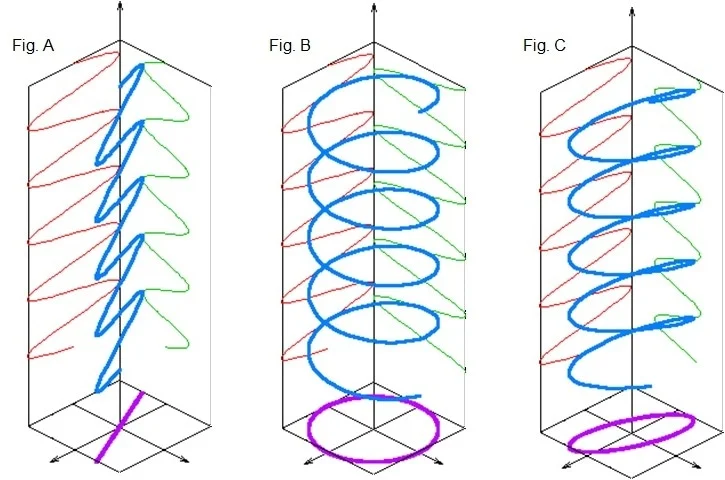
Figures A, B & C: light polarization. Image Credit: Wikipedia
Measured Quantities
Because it is an optical method, ellipsometry is non-contact and does not cause any damage to a sample. Ellipsometry can be used to analyze the thickness and optical purposes of each individual layer present within a multilayer structure.
This method is extremely sensitive because it analyzes a light beam’s phase shift as this is transported through a structure of layers. Phase angle analysis is not reliant on the absolute intensity of light.
It is possible to collect spectral data from the sample by using sources of white light and monochromators. Measurements acquired via each parameter provide information on the layer structure’s physical properties, for example, the thickness of layers and the refractive index.
This information is provided in an unpredictable manner, however.
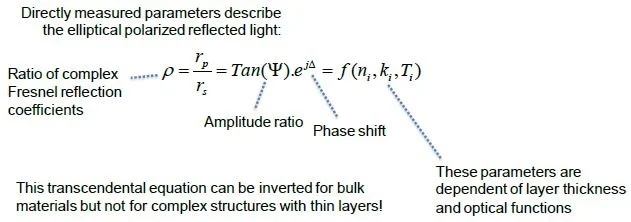
Measuring the ratio of the complex Fresnel reflection coefficients is one possible solution. Because this number is complex, it may be divided into an amplitude term and a phase shift term. Both of these terms relate to the implied ellipsometric angles, Ψ and Δ.
The Fundamental Equation of Ellipsometry
It is possible to employ precisely measured parameters in order to outline the elliptical polarized reflected light.
A model-based indirect numerical calculation may facilitate analysis of complex multi-layered structures and their properties.
Here, layer structure is taken into account, with optical functions and thickness serving as parameters.
Relative phase shift is calculated and compared against these measured parameters. This process involves the numerical regression procedure explored below.
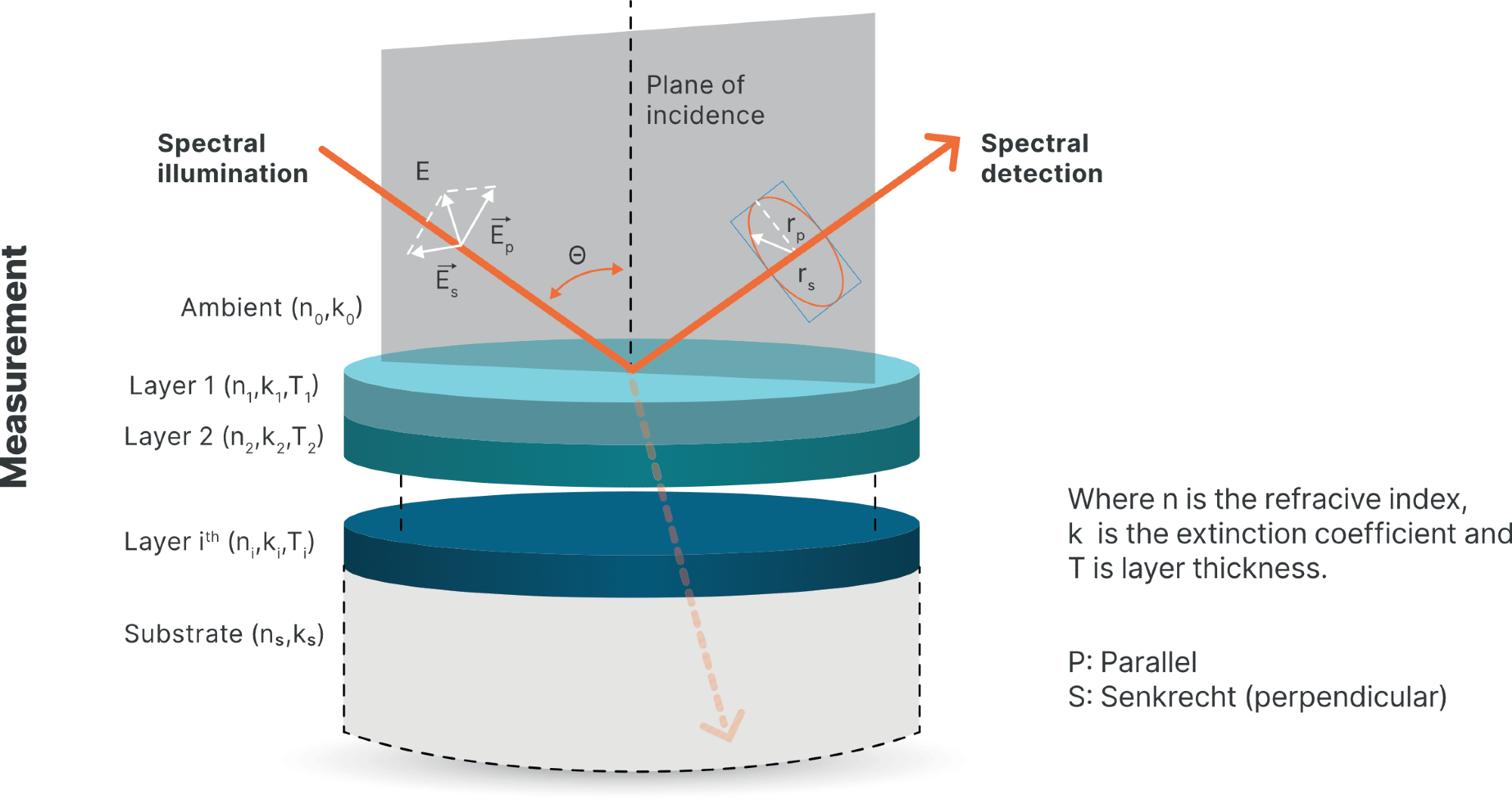
Image Credit: Semilab Semiconductor Physics Laboratory
Numerical Regression Procedure Based on an Optical Model
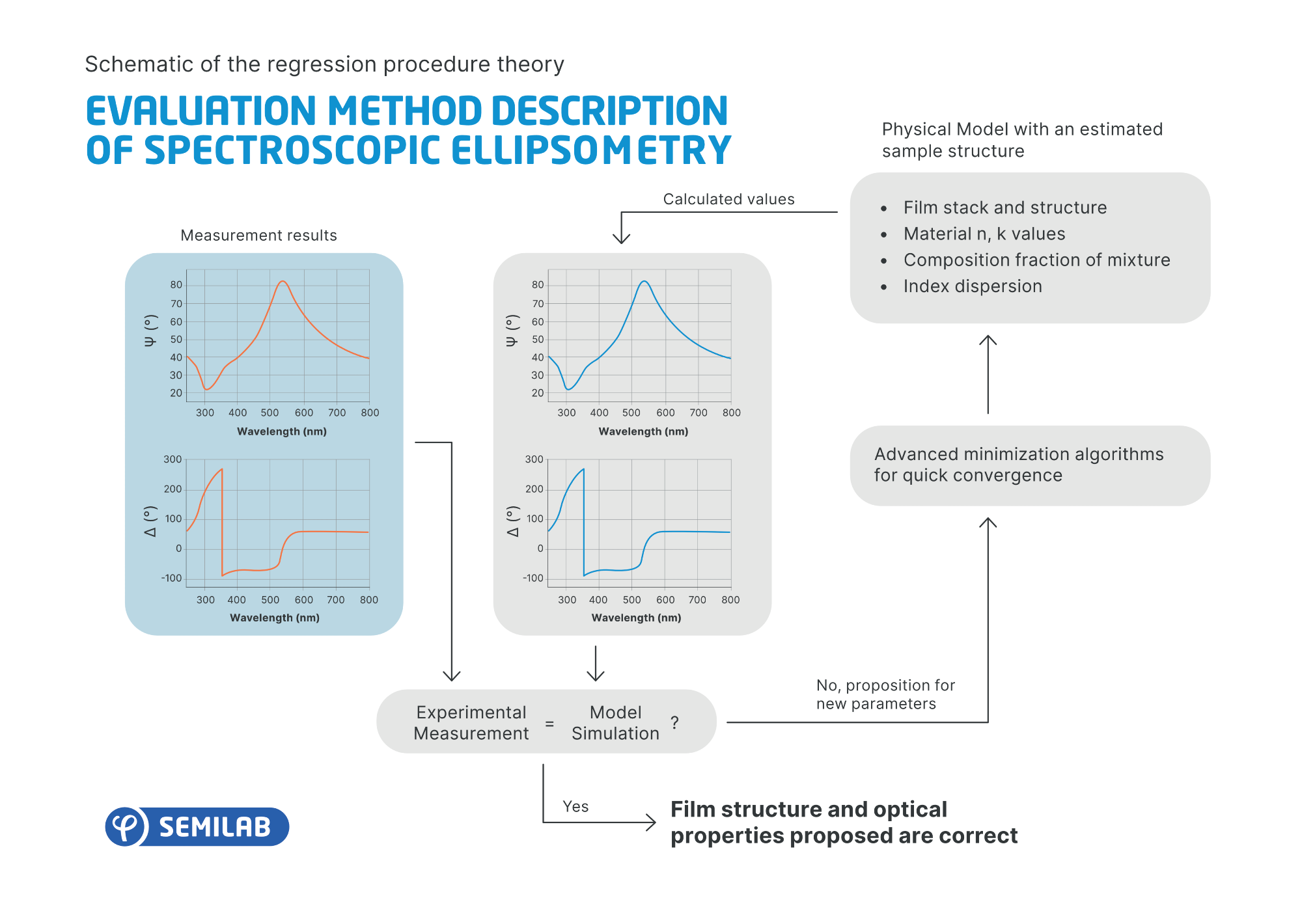
Image Credit: Semilab Semiconductor Physics Laboratory
Advanced Formalism
The state of polarization for a completely polarized light beam can be outlined somewhat through the use of Jones vectors; for example, Ex, Ey components.
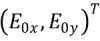
A 2x2 element referred to as a ‘Jones Matrix’ can be used to illustrate a variation of the Jones vector after reflection from a sample structure has occurred. It is possible to characterize a shift from a linearly polarized state to an orthogonal state via the formula below.
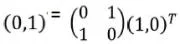
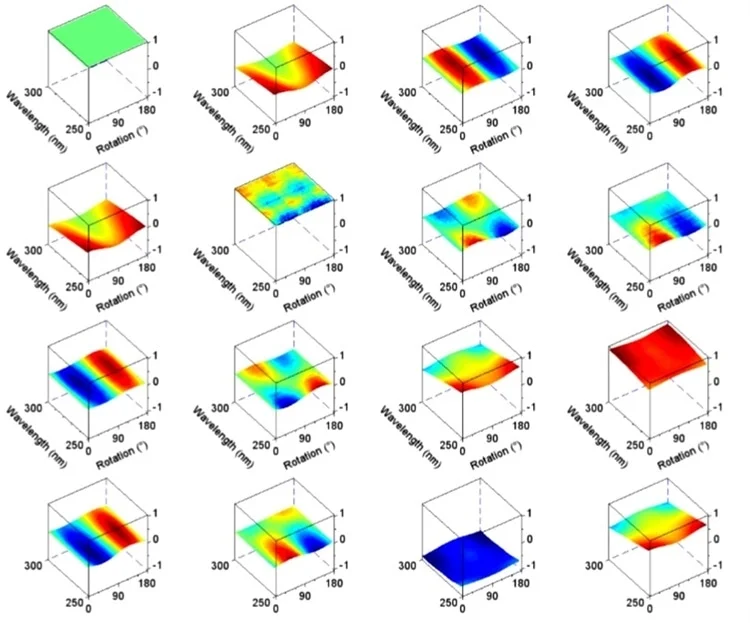
Example: Mueller Matrix of an optically active sample measured vs. stage azimuth rotation. Revealing rotational symmetry of molecular composition.* (*Example measurement: Monomolecular organic coating on solid substrate—Semilab measurement in cooperation with EPFL). Image Credit: Semilab Semiconductor Physics Laboratory
Mueller Matrix formalism founded on the 4D Stokes vectors is more commonly used to outline moderately polarized light beams.
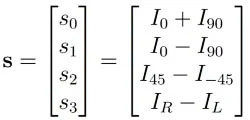
In the example shown here, S0 represents the light intensity as a whole, while S1 represents the variation in intensity between the vertical and horizontal polarization. S2 represents the variation in intensity between linearly polarized components in +45° and –45° directions, while S3 represents the variation in intensity between the left and right oriented circularly polarized components.
Multiplying the inbound light’s Stokes vector by the material’s Mueller Matrix results in the Stokes vector illustrating the reflected light:
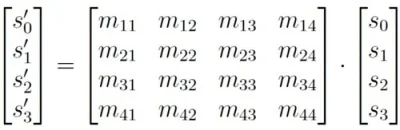
Once the Stokes vector of the inbound and reflected light has been measured, the material’s Mueller Matrix can be analyzed. This facilitates the analysis of material properties through the utilization of Mueller Matrix elements.
The material’s optical symmetries are reflected by the symmetry of the Matrix. This approach is more commonly employed as a qualitative means of analyzing an optically active sample because this approach is used without complex optical modeling of the measurement information.
Instrumentation
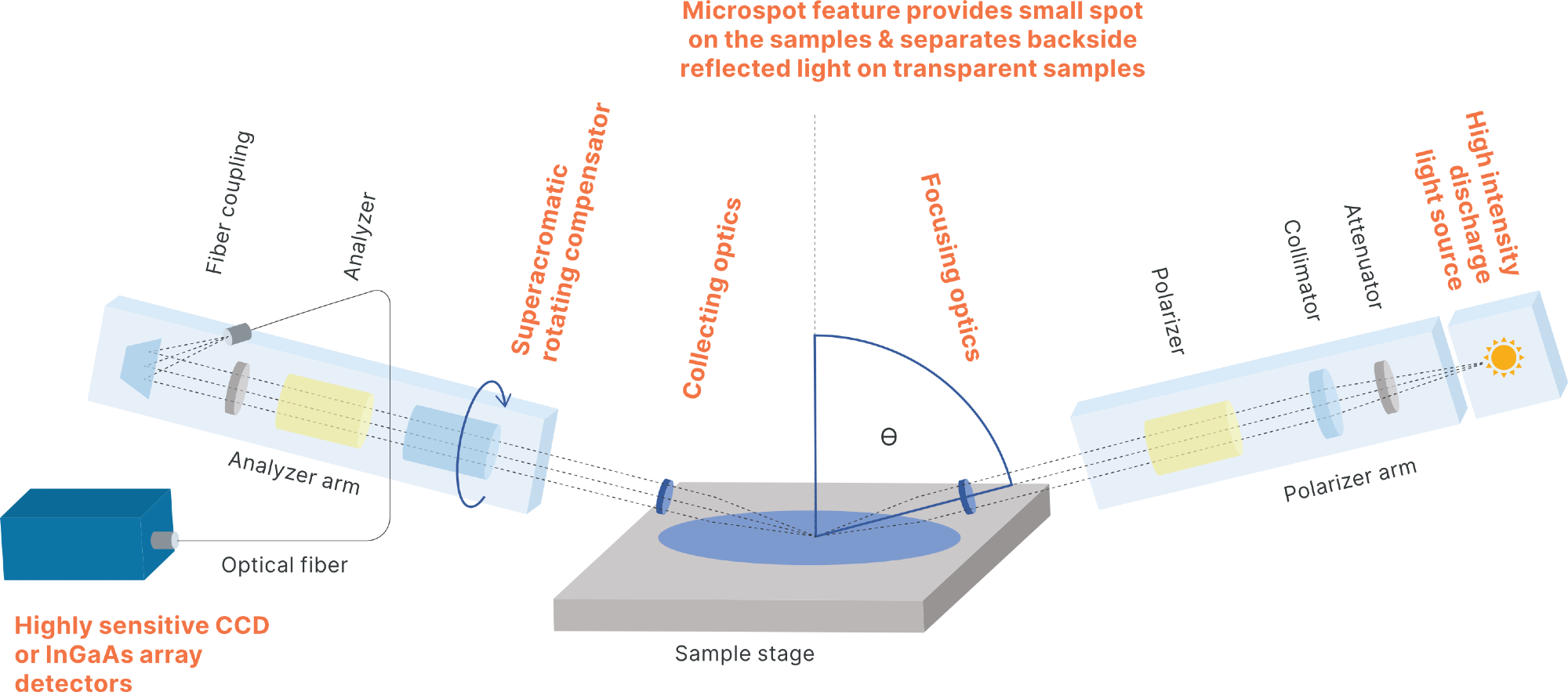
Image Credit: Semilab Semiconductor Physics Laboratory

This information has been sourced, reviewed and adapted from materials provided by Semilab Semiconductor Physics Laboratory.
For more information on this source, please visit Semilab Semiconductor Physics Laboratory.