Modal testing is a highly respected method for extracting modal parameters, for example, modal damping factors, natural frequencies, and vibration mode shapes from structures. In this example, the method is applied to a comparably recent percussion instrument known as the steelpan.
Also referred to as the Caribbean steel drum or pan, the steelpan originated in Trinidad and Tobago at the time of the Second World War. In this investigation, modal testing is performed on a soprano pan to acquire mode shapes and resonant frequencies, along with providing a spatial illustration of modal tuning in the instrument.
The response of a soprano pan excited with a periodic chirp signal from a loudspeaker was recorded by a 3-Dimensional scanning laser Doppler vibrometer.
The results show the almost harmonic relationship among tuned modes in each outer note. There is also extensive modal coupling between adjacent notes that have frequencies which are harmonically related.
Introduction
With modal testing being utilized to discover the vibrational behavior of steel pans, the instrument has become the object of significant research over the past three decades.
Despite this, modal testing on steel pans has been mostly restricted to the use of time-averaged holographic interferometry and there is a range of studies which have utilized this method to study the instrument [1-13].
This technique provides high spatial resolution however, modal parameters like damping cannot be directly acquired from this technique. Modal analysis has also been significantly used to discover the dynamic behavior of various alternative musical instruments [14-19].
Alternative modal testing methods use impact excitation or sinusoidal excitation (either acoustic or mechanical). Each of the techniques commonly include an accelerometer which is fixed to the structure as a means to detect vibration response.
The structure is tapped at several points on a grid with a hammer containing a force transducer in modal testing with impact excitation. The acceleration and force data is utilized to make a transfer function where multiple algorithms can be used to extract mode shapes and additional modal parameters [20;21].
In regards to these techniques, the critical challenge is that the incorporation of the accelerometer can cause a reduction in the values of the normal mode frequencies along with the addition of damping to the structure.
If the accelerometer is located on one of its nodal lines, a mode may also be impossible to detect. While mode shapes may be correctly determined, the spatial resolution provided by these techniques is normally poor.
In this study, a loudspeaker is used in combination with a 3D scanning laser Doppler vibrometer.
Similar to time-averaged holographic interferometry, this technique also provides high spatial resolution along with providing data from which modal damping can be inferred. This method additionally enables the observation of vibration behavior without any contact with the steelpan.
The Steelpan – A Brief History
A relatively new percussion instrument called the steelpan, also referred to as the Trinidad pan or the Caribbean steel drum, originated from a process which was heavily influenced by the drumming traditions of West African slaves who were transported to Trinidad and Tobago to work on plantation estates.
Congo drums were played by earlier generations of slaves, however, these were eventually prohibited by the government, out of anxieties that the use of these instruments could incite a rebellion.
Despite this, the emergence of a new instrument came from their love for music which took the form of bamboo poles known as tamboo-bamboo. The term originates from the French word ‘tambour’ meaning drum. This was also prohibited as clashes between rival bands led to the bamboo poles being used as fighting sticks.
The people had a great passion for music and therefore began to use dustbins, car rims, car fenders, and garbage tins as instruments. However, this was quickly replaced as the increasing oil industry and the American Naval bases in Trinidad and Tobago supplied a host of used oil drums which were utilized as a raw material for musical experimentation.
The first generation of steel pans were brought to the streets of Port-of-Spain in the Carnival celebrations a few years after the end of World War II. Since then, the steelpan has developed into a family of instruments including tenor or soprano pans, double second pans, guitar, bass, and cello pans containing a musical range that covers five octaves.
A short outline on the production of the steelpan can be read in the paper on the Aubrapan which is also a segment of this conference proceeding.
A detailed history of the instrument can be seen in Blake [22]. In this investigation, a soprano pan (Figure 1) is utilized as it has the largest amount of notes and it is probable to include the majority of the vibration features found in alternative types of pans.
Experiment
A soprano pan produced and tuned by pianist and tuner, Aubrey Bryan, was used in this investigation.
Adopting the Trinidad 4th’s and 5th’s note layout, the steelpan notes are categorized into three rings: the inner ring, the outer ring, and the middle ring. The lowest frequency note on the pan is the C4. The experimental setup used in this work is presented in Figure 3.
Foam wrapping was utilized to isolate the pan periphery from the frame surface and the soprano pan was mounted on an open chassis frame for 3-dimensional measurement of motion. The loudspeaker was held underneath the frame to generate excitation.
Situated between the three tripod-mounted sensor heads, the surface of the steelpan was coated with a thin dusting of chalk powder (developer spray) to decrease the reflection of light and to maximize the scattering of the laser signal back to each sensor head.
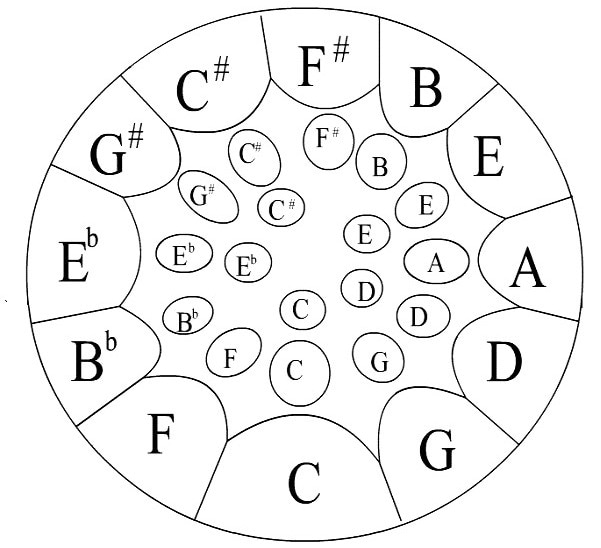
Figure 1. Note layout of soprano pan utilized in the experiment.
The loudspeaker played periodic chirp across the acoustic frequency region to excite steelpan vibrations and all possible modes in the structure.
A remote loudspeaker was selected as this technique of excitation prevents any modification of the structural response either globally or locally as a result of physical contact with the pan surface by a stinger connected vibrator or striker.
An enhanced uniformity of excitation was also a positive outcome as the loudspeaker excitation was spread over the steelpan surface.
It was also more possible to control excitation as the loudspeaker was managed by a repeatable electrical signal from an included function generator whose frequency was the same as the FFT and bandwidth settings of the Polytec 3D scanning laser system.
The volume needed to be high (approximately 95 dB) for successful excitation because the excitation was air-coupled and was located at a distance away from the drum surface. This meant that performing the experiment was impossible throughout standard hours of work. Therefore, the system was left to automatically record and scan the drum response throughout the late-evening.
The pan response was analyzed using a Polytec 3-Dimensional scanning vibrometer laser system comprising of three distinct sensor heads or lasers that take measurements of surface velocity from various directions (shown in Figure 3).
This enables motion components to be extracted along with three perpendicular directions. The system measured out-of-plane (flexural) and in-plane (extensional) pan vibrations in the form of mobility over the complete pan surface. The system additionally analyzed the geometry of the steelpan dish.
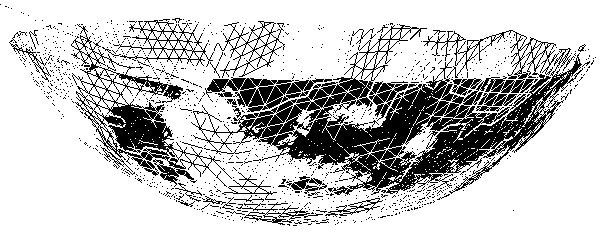
Figure 2. Scanned geometry of pan dish.
The configurations for the 3-Dimensional scan were for a frequency bandwidth of 5 kHz with a resolution of 1.5625 Hz (3200 FFT lines), analyzing 7420 points with five averages. The measurement was achieved with 99.8% of points returning a high-quality status.
The collected vibration data was employed to develop animations of mode shapes for each of the note regions on the surface of the pan. The laser vibrometer measures the frequency of the vibrating surface by using the Doppler effect. The change in the signal beam frequency (fs) corresponds to the velocity (v) of the vibrating surface and the wavelength (λ) of the laser in the following equation:
 |
(1) |

Figure 3. Set-up of the tri-laser system for the 3- dimensional scans of the soprano steelpan.
Results and Discussion
The initial vibration modes of the C4# note region are demonstrated in Figure 4. The mode designation (m,n) will be employed where m provides the number of radial nodes and n provides the number of circumferential nodes.
The fundamental or lowest mode (0,0) at 276 Hz signifies the vibration of the complete note area in a single phase. The (0,1) mode was analyzed at 550 Hz and the (1,0) mode at 640 Hz. The second and third modes have frequencies at an estimated 2.0 and 2.3 times the fundamental mode’s natural frequency.
These ratios are an octave and approximately a major third greater an octave. All the alternative outer notes on the pan exhibited the same frequency relationships and mode shapes. These initial three modes are normally tuned into a harmonic relationship (see Figure 6).
In this event, the third mode fails to fall into a harmonic series. Despite this, its ratio to the fundamental is one which is attractive to the human ear. Certain tuners can tune the third mode in such a way that the ratio to the fundamental is 3:1. Figure 4b also illuminates an additional characteristic of the instrument.
The fundamental mode (0,0) frequency of the C5# note is equal to the (0,1) mode for the C4# note. This is commonly seen whenever modes contain frequency values that are in close proximity. Figure 4c also evidences this where the (1,0) mode of C4# and the (0,0) mode of E5b vibrate at 640 Hz. The (0,0) mode of the E5b is also noted at 632 Hz.

Figure 4. The first three flexural modes of the C4# note region: (a) 276 Hz, (b) 550 Hz and (c) 640 Hz.

Figure 5. Modal Coupling in soprano pan: This is a result of the presence of partials of the same frequency in various note regions: (a) 681 Hz, (b) 1067 Hz, (c) 1252 Hz and (d) 1359 Hz.
Every mode seen in the frequency range of interest were flexural modes, showing that most of the sound generated from the instrument is mainly caused by flexural motions of the note regions. Regardless, some radiation of sound is predicted to occur from the pan side because it is coupled to the pan dish.
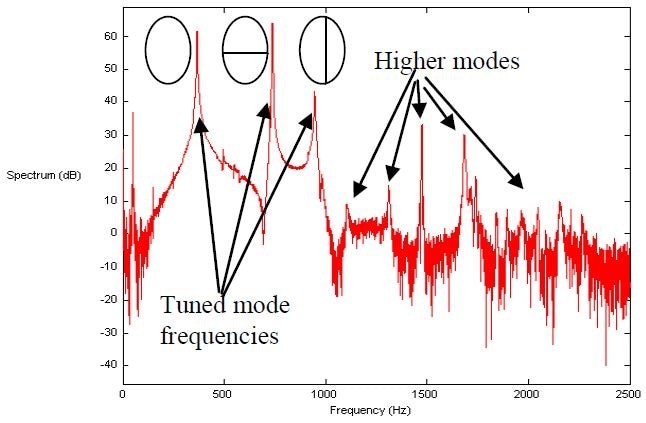
Figure 6. Common frequency response spectrum for an outer note on the soprano pan. First three modes are normally tuned into an almost harmonic relationship. Higher modes are not harmonic but enhance the overall timbre of the steelpan. Acquired utilizing the 1D scanning laser Dopler vibrometer and excitation as a product of an impact hammer.
This study mostly observed mode shapes in the steelpan with the purpose of gaining information about modal tuning, however other practical information can be acquired by combining the measurements collected in this study with other measurements, for example, acoustic measurements.
The information collected from this investigation are as follows: averaged mobilities (m/s/V), normal mode frequencies, along with in-plane and flexural motion. It was also easy to extract damping properties.
Further information, for example, radiation damping and radiation efficiency can be acquired with acoustic measurements. The 3D measurements additionally produce a 3-dimensional mesh of the steelpan which may be utilized to carry out finite element simulations (see Figure 2).
Conclusion
Modal testing of the soprano pan has given a spatial illustration of mode tuning in the instrument. Pan-makers frequently tune the first three modes of notes on the outer ring to have frequencies that create an estimated harmonic sequence. The fundamental mode is the only mode to be tuned in the inner and middle notes.
Additionally, there was extensive mode coupling within notes which held partials of equal frequency. Even though modal testing of the steelpan is not recent, modal testing with a 3D scanning laser Doppler vibrometer provides further features which can be utilized in combination with finite element analysis and acoustic measurements to perform a complete investigation.
References and Further Reading
[1] Barlow, C.Y., et al., The Caribbean Steel Drum. Proceedings of the Institute of Acoustics, 1988: p. 193- 198.
[2] Hansen, U.J. and T.D. Rossing, Modal analysis of a Caribbean steel drum. The Journal of the Acoustical Society of America, 1987. 82(S1): p. S68-S68.
[3] Hansen, U.J. and T.D. Rossing, Modal studies in a double second Caribbean steel drum. The Journal of the Acoustical Society of America, 1989. 85(S1): p. S32-S32.
[4] Hansen, U.J. and T.D. Rossing. The Caribbean Steelpan, and some offsprings. in Forum Acusticum. 2005. Budapest.
[5] Hansen, U.J., et al., The Caribbean Steel Pan: Tuning and Mode Studies. MRS Bulletin, 1995. 20(3): p. 44- 46.
[6] Rossing, T.D. and D.S. Hampton. Modal analysis of musical instruments with holographic interferometry. 1991. Rosemont, IL, USA: Publ by Int Soc for Optical Engineering, Bellingham, WA, USA.
[7] Rossing, T.D., D.S. Hampton, and J. Boverman, Acoustics of Caribbean steel drums. The Journal of the Acoustical Society of America, 1986. 80(S1): p. S102- S102.
[8] Rossing, T.D., D.S. Hampton, and U.J. Hansen, Music from oil drums: The acoustics of the steel pan. Physics Today, 1996. 49(3): p. 24-29.
[9] Rossing, T.D., D.S. Hampton, and U.J. Hanson, Acoustics of Steelpans, in 130th meeting of ASA. 1995.
[10] Rossing, T.D. and U.J. Hansen, Vibrational mode shapes in Caribbean steelpans Part II: cello and bass. Applied Acoustics, 2004. 65: p. 1233-1247.
[11] Rossing, T.D., U.J. Hansen, and D.S. Hampton, Vibrational mode shapes in Caribbean steelpans. I. Tenor and double second. Journal of the Acoustical Society of America, 2000. 108(2): p. 803-812.
[12] Rossing, T.D., et al., The Caribbean Steelpan: Tuning and Mode Studies. MRS Bulletin, 1995. 20(3): p. 44- 46.
[13] Rossing, T.D., U.J. Hansen, and D. Scott Hampton. Modal analysis of steelpans: holographic, computer, sand patterns, and microphone scanning. in Proceedings of the 1st International Conference on the Science and Technology of the Steelpan. 2000. Port-ofSpain, Trinidad: 73-82.
[14] Bork, I., Practical tuning of xylophone bars and resonators. Applied Acoustics, 1995. 46(1): p. 103- 127.
[15] Bork, I., et al., Comparison between Modal Analysis and Finite Element Modelling of a Marimba bar. ACUSTICA.acta acustica, 1999. 85: p. 258-266.
[16] Bretos, J., C. Santamaría, and J. Alonso Moral, Finite element analysis and experimental measurements of natural eigenmodes and random responses of wooden bars used in musical instruments. Applied Acoustics, 1999. 56(3): p. 141-156.
[17] Bretos, J., C. Santamaría, and J.A. Moral, Frequencies, input admittances and bandwidths of the natural bending eigenmodes in xylophone bars. Journal of Sound and Vibration, 1997. 203(1): p. 1-9.
[18] Bretos, J., C. Santamaría, and J.A. Moral, Tuning process of xylophone and marimba bars analysed by the finite element modeling and experimental measurements. Journal of the Acoustical Society of America: Technical Notes and Research Briefs, 1997. 102(6): p. 3815-3816.
[19] Perrin, R., T. Charnley, and J. dePont, Normal modes of the modern English church bell. Journal of Sound and Vibration, 1983. 90(1): p. 29-49.
[20] Ewins, D.J., Modal Testing: Theory, Practice and Application 2nd ed. 2000, Baldock: Research Studies Press Ltd.
[21] Heylen, W., S. Lammens, and P. Sas, Modal Analysis Theory and Testing. 2003, Leuven: Katholieke Universiteit Leuven.
[22] Blake, F.I.R., The Trinidad and Tobago Steel Pan: History and Evolution. 1st ed. 1995, Port of Spain: Speeds Printery.

This information has been sourced, reviewed and adapted from materials provided by Polytec.
For more information on this source, please visit Polytec.